行波过程分析的网格图法

网格图法是分析传输线行波过程的有力工具。网格图有时间与距离两个座标。它反映了任一瞬间线路入射波、反射波与透射波的位置与运动方向，形象直观，易于理解。根据行波过程的网格图，可求出线路上任一点电压、电流随时间的变化情况。

下面用两个具体的例子说明网格图的应用。

 1. 直流电压突然作用于空载线路

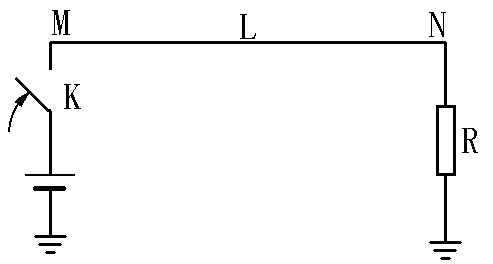
如图2.14.a所示，t=0，开关K合上，电压为E的直流电压源与长度等于L的空载长线MN接通，线路N端接有电阻R，R是线路波阻抗值的二倍，因此N端的电压反射系数ρN=1/3。    

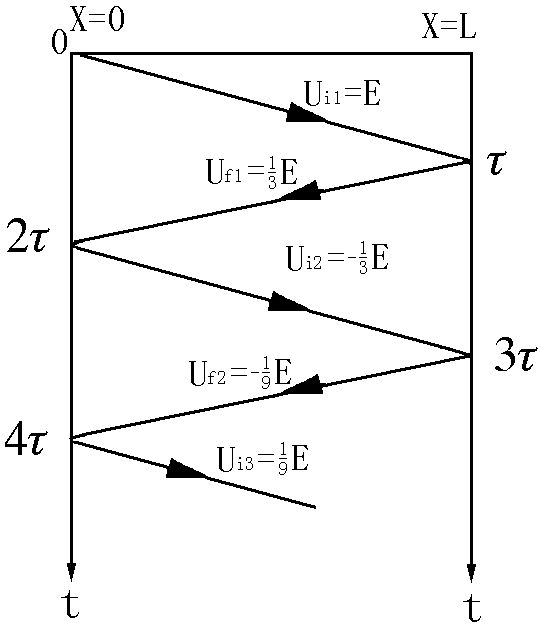
图2.14.b给出了电压行波传播网格图，横座标X代表距离，X=0与X=L对应线路的两个端点，由X=0，X=L处分别作垂直于X轴的直线作为时间t轴。

    t=0，K合上，电压波Ui1=E以波速V向N端运动，用从M处时间轴t=0出发向下运动的斜线来代替，斜线代表的电压值不变，箭头指向N端代表入射波的运动方向。斜线上某一点座标为（t0、 x0），代表在t0时刻，电压行波运动到了线路上距离M端X0的位置，斜线与X=L处时间轴的相交点即电压波运动到N端所需时间τ(τ=L/V，是行波在整个线路上的传播时间)。电压行波运动到N端后产生反射电压Uf1返回M点，在图上用从N处时间轴t=τ点出发的斜线表示，反射电压等于N端电压反射系数乘以入射电压，即Uf1=ρNUi1=E/3。Uf1在t=2τ时到达M点，由于M点接有直流电压源，内阻为0，对于入射电压波来说相当于短路，反射系数为-1，故产生反射波Ui2=-Uf1=-E/3向N点运动。t=3τ时刻Ui2到达N点，产生反射波Uf2=ρNUi2=-E/9又向M点运动……，电压行波这样在M与N点来回运动，直至整个过程结束，形成了锯齿形的网格图。

根据网格图，可以很方便地求出线路上任一点在任一时刻的电压、电流值。首先在时间轴上找到所研究的时间t，然后把该时间前出现的所有的电压、电流波求和即可。

（a）

(b)

图2.14  直流电压突然作用于空载线路网格图

例如求N点电压变化规律，t=τ之前，N端无电压波出现，UN=0，而在τ〈t〈3τ期间，N点有来自M方向的入射波Ui1,与向着M点运动的反射波Uf1,故：

UN=Ui1+Uf1=E+(E/3)=4E/3

而在3τ〈t〈5τ期间，线路上存在Ui1、Uf1、Ui2、Uf2四个电压波，它们的和是8E/9；依次类推，求出5τ时刻之后的UN，如图2.15。

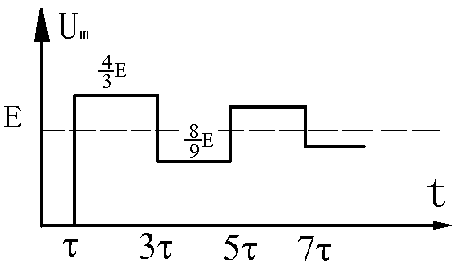
图2.15  线路M点电压波形

随着时间的增大，可以证明UN趋近于稳定值E，因此有：

2. 向低电阻故障电缆注入幅值为E的直流电压

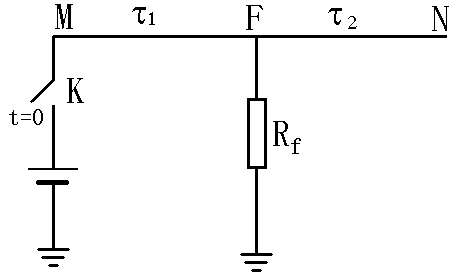
如图2.16.a 所示，电缆中间F点发生低电阻故障，F点到电缆两端点的距离分别为L1、L2，传播时间分别为τ1与τ2(τ1〈τ2)。电缆N点开路，电压反射系数ρN=1；由于直流电压源作用于M端，电压反射系数为ρM=-1；故障点反射系数与透射系数分别为ρF与γF。由于电缆中存在低电阻故障，任意电压波U到达F点后，除产生反射波ρFU外，还有透射波γFU继续往前运动，对应的行波网格图如图2.16所示，各个电压行波的数值均标在了对应的斜线上方。

                         a

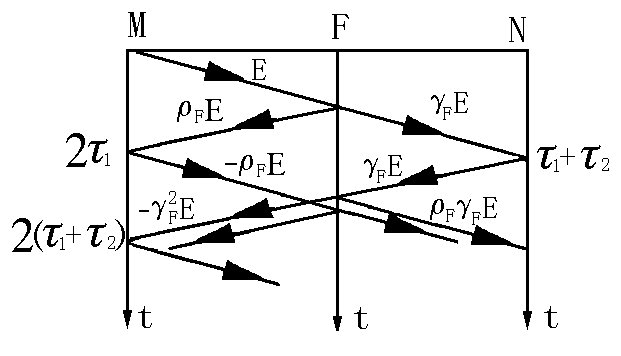
b

图2.16  向低电阻故障电缆注入直流电压

光大百纳--专注电缆故障检测