电缆故障检测行波的反射系数

电缆故障检测时行波的反射程度可用发生反射的阻抗不匹配点的反射电压(电流)与入射电压(电流)之比来表示,这比值称为反射系数。设线路波阻抗为Z1，阻抗不匹配点等效阻抗为Z2，见图2.5,则电压反射系数为:

ρu=Uf/Ui =(Z2-Z1)/(Z2+Z1)                (2.3)

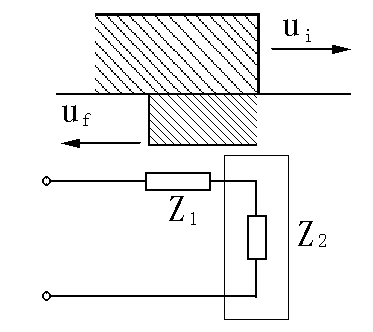
图2.5  行波的反射

假定入射波是正向行波,则入射电压与电流波的关系:

         ii=Ui/Z0                          (2.4)

而对应的反射波是反向行波,反射电压与电流波的关系:

         if = -Uf/Z0                        (2.5)

由式2.3、2.4、2.5 推出,阻抗不匹配点的电流反射系数:

         ρi=if/ii=-Uf/Ui=-ρu

可见,阻抗不匹配点的电流反射系数与电压反射系数大小相等,符号相反。

下面讨论电缆故障检测时几种情况下的反射系数。

1. 开路

当电缆出现开路点,或行波运动到电缆的开路终端时, Z2→∞。根据式2.3,由于Z1远小于Z2,可以忽略Z1的作用,求出电压反射系数:

         ρu=1

开路造成了电压的全反射(图2.6),电压反射波与入射波同极性。实际的开路点电压是入射电压与反射电压之和,因此出现了电压加倍现象。

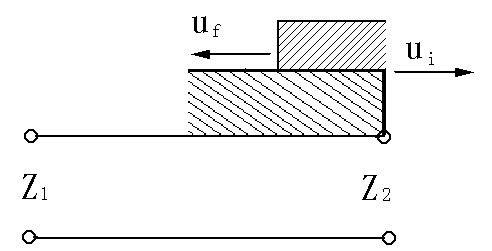
图2.6 开路端的电压反射

开路点的电流反射系数为-1,反射电流与入射电流大小相等,方向相反,实际的开路点电流是二者之和,因此为零。

开路点的电流为零,电压加倍,可解释为行波达到开路点后,由电流携带的磁场能量全部转化为由线路电压所代表的电场能量。

2. 短路

当电缆中出现短路点时,Z2=0,根据式2.3,求出电压反射系数:

                ρu=-1

短路点反射电压与入射电压大小相等,方向相反(图2.7),其合成电压为零。

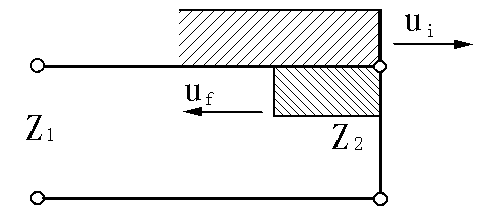
图2.7 短路点的反射

短路点电流反射系数为+1,反射电流与入射电流相等,短路点出现电流加倍现象。

短路点电压为零,电流加倍,说明行波到达短路点后,电场能量全部转化成了磁场能量。

3. 电缆中出现低阻故障

电缆中间出现低阻故障时,见图2.8,电阻两边的电缆分别用大小等于波阻抗值Z0的电阻来代替, 故障电阻Rf与第二段电缆的波阻抗值Z0相并联,构成了第一段电缆的负载阻抗,即:

           Z2= RfZ0/(Rf+Z0)                   

故障点电压反射系数:

         Pu=(Z2-Z1)/(Z2+Z1)=-1/（1+2K）       (2.6)

其中K=Rf/Z0。

式2.6对于分析低压脉冲在故障点的反射特别有用。

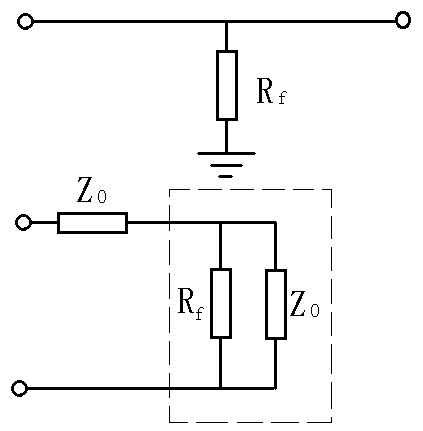
图2.8  电缆低阻故障点等效电路

4. 电感

当电缆负载为一电感时，见图2.9，反射系数不再是一简单的实数，而是一随时间变化的量。

可以推出电压反射系数为：

            ru=2e- t/τ - 1                (2.7)

其中τ=L/Z0,称为时间常数，L为电感值。

        t=0 ,        ρu=1

        t=τ,        ρu=-0.26

        t→∞ ,      ρu=-1

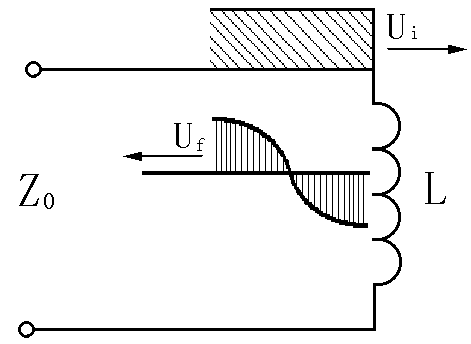
图2.9  电感的反射

可见，终端接电感后，电压反射系数ρu将随时间由

+1向-1变化。因为t=0时，电压波刚到达电缆终端，因电感上电流不能突变，电感相当于开路，故反射系数ρu=1；而t→∞时，电感上电流进入稳态，电压为零，相当于短路，因此ρu=-1，见图2.10。电压反射系数为零的时间，t0=τln2 。

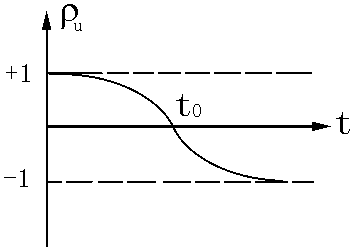
                  图2.10  电感的反射系数

5. 电容

终端接电容时，图2.11，推出电压反射系数：

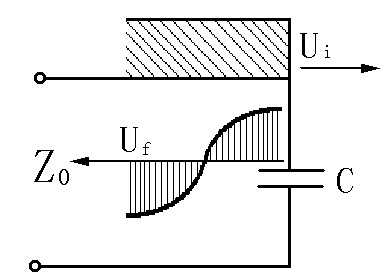
图2.11  电容的反射

          ρu=1-2e- t/τ

其中τ=Z0C，称为时间常数，C为电容值。

可见终端接电容时，反射系数随时间从-1向+1变化，t=0时，电容上电压不能突变，相当于短路，故反射系数ρu=-1，而当t→∞时，电容上电压已稳定，相当于开路，故反射系数为1，见图2.12。

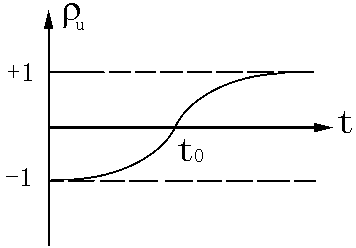
图2.12  电容的反射系数

光大百纳--专注电缆故障检测